Microsoft Rewards quizzes, like those from April 5th, 2024, and February 4th, 2025, demonstrate engaging online activities. These quizzes, often involving daily answers,
provide points and a green checkmark upon completion, though occasional bugs may occur.
What are Exponential Functions?
Exponential functions represent growth or decay, mirroring the dynamic nature of online reward systems like Microsoft Rewards, as discussed on December 4th, 2021. These functions feature a constant base raised to a variable exponent. Think of accumulating points – initial rewards (like the 10 points mentioned on April 5th, 2024) can grow exponentially with continued participation.
Unlike linear functions with a constant rate of change, exponential functions exhibit a rate of change proportional to the current value. This is akin to a popular recipe, like the Buffalo Chicken Dip detailed on February 7th, 2025, where flavors intensify with baking. The core concept involves repeated multiplication, leading to rapid increases or decreases, crucial for understanding various real-world phenomena.
The General Form of an Exponential Function
The standard form of an exponential function is y = a * bx, where ‘a’ represents the initial value and ‘b’ is the base. Similar to tracking points in Microsoft Rewards (referenced on December 30th, 2025), ‘a’ signifies your starting amount, while ‘b’ dictates the growth or decay rate.
If ‘b’ is greater than 1, the function represents exponential growth – points accumulate faster, like a delicious Buffalo Chicken Dip (February 4th, 2025) gaining flavor. If ‘b’ is between 0 and 1, it signifies exponential decay, a diminishing return. Understanding this form is vital, as it allows us to analyze and predict the behavior of these functions, much like anticipating rewards from completing online quizzes.

Graphing Exponential Functions: Key Concepts
Like completing Microsoft Rewards quizzes (December 4th, 2021), graphing requires understanding key elements: asymptotes, the base’s impact, and the ‘a’ value’s role.
Understanding Asymptotes
Asymptotes are crucial when graphing, much like navigating Microsoft Rewards quizzes with potential bugs (reported December 4th, 2021). In exponential functions, a horizontal asymptote represents a value the function approaches but never quite reaches. For functions like y = bx, the asymptote is typically y = 0. This is because as x approaches negative infinity, the function gets infinitely close to zero.
Transformations, such as adding a constant to the function (y = bx + a), shift the asymptote vertically to y = a. Understanding this shift is vital, similar to needing the correct answers on a quiz to earn points. Recognizing the asymptote helps define the function’s behavior and accurately sketch its graph, avoiding common errors.
The Role of the Base (b)
The base, ‘b’, in the exponential function y = bx, dramatically influences the graph’s shape, much like completing Microsoft Rewards quizzes (mentioned February 7th, 2025) impacts your points. If b > 1, the function represents exponential growth – the graph increases rapidly as x increases. Conversely, if 0 < b < 1, the function represents exponential decay, decreasing rapidly.
A larger base leads to faster growth or decay. For example, 2x grows slower than 3x. The base determines whether the curve is steep or relatively flat. Misinterpreting the base, as cautioned in common errors, can lead to an inaccurate graph, similar to selecting incorrect answers on a quiz.
Impact of ‘a’ in y = a * b^x
Impact of ‘a’ in y = a * bx
The coefficient ‘a’ in the equation y = a * bx introduces a vertical stretch or compression, akin to earning bonus points on Microsoft Rewards quizzes (discussed on December 4th, 2021). If |a| > 1, the graph is stretched vertically, making the growth or decay more pronounced. If 0 < |a| < 1, the graph is compressed vertically, lessening the effect.
A negative value for ‘a’ reflects the graph across the x-axis. ‘a’ doesn’t alter the asymptote but changes the y-intercept. Understanding ‘a’ is crucial for accurate graphing, avoiding errors like incorrectly identifying the asymptote, and achieving a correct solution, much like completing a quiz accurately.

Step-by-Step Graphing Process
Like completing Microsoft Rewards quizzes (mentioned on February 7th, 2025), a methodical approach is key. Follow defined steps for accurate results and understanding.

Step 1: Identifying Key Parameters
Beginning, much like tackling Microsoft Rewards quizzes (as discussed on December 4th, 2021), requires careful observation. First, isolate the base ‘b’ within the exponential function, y = a * bx. This base dictates the growth or decay rate. Next, pinpoint ‘a’, which governs vertical stretching or compression and any vertical shifts.
Recognize that a value of ‘a’ greater than one stretches the graph, while a value between zero and one compresses it. Pay attention to the sign of ‘a’; a negative ‘a’ reflects the graph across the x-axis. Finally, understand that the exponent ‘x’ is crucial, and the function’s behavior is fundamentally tied to the base ‘b’. Correctly identifying these parameters is foundational for accurate graphing, similar to getting the right answers on a quiz!
Step 2: Plotting Initial Points (x=0)
Similar to completing a Microsoft Rewards quiz and receiving immediate feedback (as noted on April 5th, 2024), starting with x=0 provides a quick initial point. Substitute x=0 into your exponential function, y = a * bx. This simplifies to y = a * b0. Remember that any non-zero number raised to the power of zero equals one.
Therefore, your y-intercept will always be ‘a’. Plot this point (0, a) on your coordinate plane. This initial point serves as a crucial anchor for sketching the curve. For example, if your function is y = 3 * 2x, your starting point is (0, 3); This initial step, like clicking the quiz tile for 10 points, is a simple but vital beginning.
Step 3: Determining the Asymptote
Just as Microsoft Rewards quizzes sometimes present unexpected challenges (documented since December 4th, 2021), identifying the asymptote requires careful attention. An asymptote is a line that the exponential curve approaches but never quite touches. For functions of the form y = a * bx, the asymptote is the x-axis (y = 0) if there’s no vertical shift.
If the function includes a vertical shift, like in y = a * bx + c, the asymptote becomes y = c. This horizontal line guides the curve’s behavior. Recognizing this, similar to finding the correct answers on a quiz, is key to accurate graphing. The curve gets infinitely close to the asymptote as x approaches negative infinity.
Step 4: Plotting Additional Points
Similar to completing Microsoft Rewards quizzes for points (as noted on February 7th, 2025), plotting additional points solidifies the graph’s shape. After establishing the initial point and asymptote, choose several x-values – both positive and negative – and calculate the corresponding y-values. Focus on values that showcase the curve’s rapid growth or decay.
For example, if b > 1, the function increases rapidly as x increases. If 0 < b < 1, the function decreases rapidly. Remember, consistency is key, much like ensuring correct answers on the Bing quizzes. These points, when plotted, will clearly illustrate the exponential trend and confirm the asymptote’s accuracy, creating a complete and accurate graph.
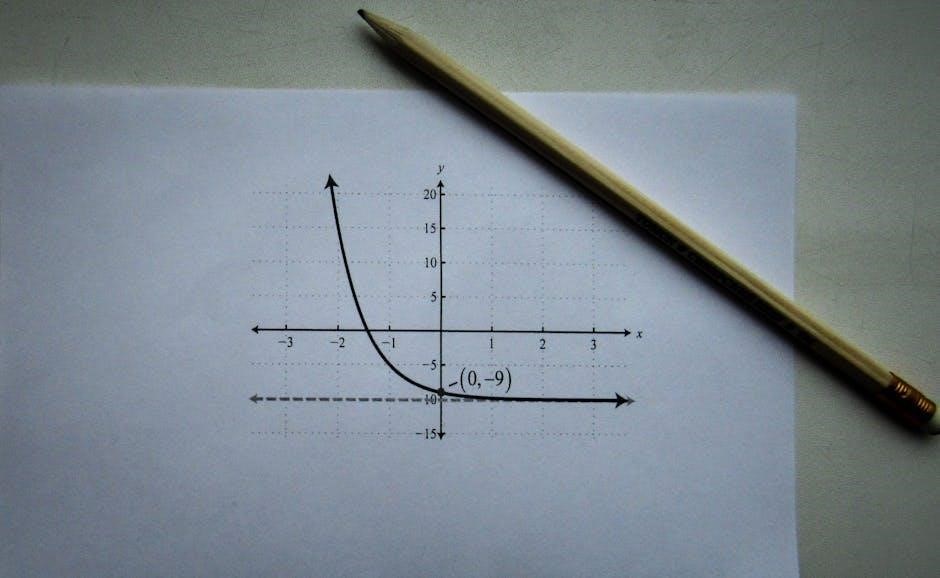
Worksheet Examples & Solutions
Like the Microsoft Rewards quizzes from December 4th, 2021, practice is crucial! These examples, with detailed solutions, build confidence in graphing exponential functions effectively.
Example 1: Graphing y = 2^x
Let’s explore graphing y = 2x. First, create a table of values. For x = -2, y = 0.25; for x = -1, y = 0.5; for x = 0, y = 1; for x = 1, y = 2; and for x = 2, y = 4.
Plot these points on a coordinate plane. Notice the curve steadily increases as x increases. The x-axis serves as a horizontal asymptote, meaning the graph approaches, but never touches, the x-axis as x approaches negative infinity.
The base, 2, is greater than 1, indicating exponential growth. As seen in Microsoft Rewards quiz discussions (Dec 4, 2021), understanding these steps is key. The graph will pass through (0,1), a crucial point for all exponential functions of this form.
Example 2: Graphing y = 3 * 2^x ― 1
Now, let’s graph y = 3 * 2x ⎯ 1. Similar to the previous example, we’ll build a table of values. The ‘3’ stretches the graph vertically, and the ‘-1’ shifts it down one unit.
For x = 0, y = 3(1) ⎯ 1 = 2. For x = 1, y = 3(2) ⎯ 1 = 5. For x = -1, y = 3(0.5) ― 1 = 0.5. The asymptote remains the x-axis, but the entire graph is now positioned differently.
Remember, as highlighted in discussions about Microsoft Rewards quizzes (April 5, 2024), careful attention to these transformations is vital. The graph passes through (0, 2) instead of (0, 1). This demonstrates the impact of the ‘a’ value in the general form.
Example 3: Graphing y = (1/2)^x + 2
Let’s examine y = (1/2)x + 2. Here, the base is less than one, indicating exponential decay. The ‘+ 2’ shifts the graph upwards by two units. For x = 0, y = (1/2)0 + 2 = 1 + 2 = 3. For x = 1, y = (1/2)1 + 2 = 0.5 + 2 = 2.5. For x = -1, y = 2 + 2 = 4.
The asymptote shifts to y = 2. Like the Microsoft Rewards quizzes mentioned on December 4th, 2021, and February 7th, 2025, accuracy is key. The graph approaches y = 2 as x approaches infinity, but never touches it.
Notice how the graph decreases as x increases, unlike the previous examples. This illustrates the effect of a fractional base.

Transformations of Exponential Functions
Buffalo chicken dip recipes, like the one from February 4th, 2025, showcase variations. Similarly, exponential functions transform via shifts and reflections, altering their graphs.

Vertical Shifts
Considering the Microsoft Rewards quizzes from December 30th, 2025, and December 4th, 2021, completing tasks often yields points, mirroring how adjustments impact exponential graphs. Vertical shifts occur when adding a constant to the exponential function, altering the horizontal asymptote. For example, in y = bx + k, ‘k’ dictates the upward (k > 0) or downward (k < 0) shift.
The entire graph moves without changing its shape. Like finding correct quiz answers, identifying ‘k’ is crucial. A positive ‘k’ raises the graph, while a negative ‘k’ lowers it. This shift doesn’t affect the domain or range, only the y-intercept and asymptote position. Understanding this is key, similar to navigating quiz bugs for rewards!
Horizontal Shifts
Reflecting on the Buffalo Chicken Dip recipes from February 7th, 2025, and October 12th, 2025, variations demonstrate adjustments – similar to horizontal shifts in exponential functions. These shifts happen within the exponent. The function y = b(x ⎯ h) shifts the graph horizontally. If ‘h’ is positive, the graph moves to the right; if negative, it moves to the left.
Unlike vertical shifts, horizontal shifts impact the domain. Like troubleshooting Microsoft Rewards quiz issues (December 4th, 2021), identifying the correct sign of ‘h’ is vital. The asymptote also shifts horizontally by ‘h’ units. Remember, these shifts don’t alter the graph’s shape or vertical asymptote, just its position along the x-axis.
Reflections
Considering the “deconstructed” Buffalo Wing Dip (October 12th, 2025), a reflection mirrors the original – a similar concept applies to exponential functions. Multiplying the entire function by -1, as in y = -bx, reflects the graph across the x-axis. This changes the sign of all y-values.
The asymptote remains unchanged, but the range is flipped. Like resolving bugs in Microsoft Rewards quizzes (December 4th, 2021), careful attention to detail is crucial. A reflection doesn’t alter the domain or the base ‘b’. If there’s already a vertical shift or stretch, the reflection applies after those transformations. Understanding this order of operations is key to accurately graphing reflected exponential functions.

Common Errors to Avoid
Like incorrect answers on Microsoft Rewards quizzes (April 5th, 2024), misidentifying the asymptote or base ‘b’ are frequent errors when graphing exponential functions.
Incorrectly Identifying the Asymptote
A common mistake, mirroring issues reported with Microsoft Rewards quizzes on December 4th, 2021, is misinterpreting the horizontal asymptote of an exponential function. Students often confuse it with the y-intercept or incorrectly assume it’s always y=0. Remember, the asymptote represents the value that ‘y’ approaches as ‘x’ tends towards positive or negative infinity.
For functions like y = a * bx + c, the asymptote is y = c. Failing to account for the vertical shift ‘c’ leads to an inaccurate graph. Furthermore, understanding that the asymptote is not crossed by the graph is crucial. Like needing correct answers for Microsoft Rewards points, precision is key. Always double-check the equation to determine the correct asymptote before plotting.
Misinterpreting the Base
Similar to encountering bugs while completing Microsoft Rewards quizzes – as noted on December 4th, 2021 – a frequent error involves misunderstanding the role of the base (‘b’) in the exponential function y = a * bx. Students sometimes incorrectly assume a larger base always means a faster-growing function, neglecting the impact of fractional bases.
If 0 < b < 1, the function represents exponential decay, and the graph decreases as ‘x’ increases. Conversely, if b > 1, it’s exponential growth. Confusing these leads to an inverted graph. Just as getting quiz answers right earns points, correctly identifying whether the base indicates growth or decay is fundamental. Remember, the base dictates the rate and direction of change.
Resources & Further Practice
Like finding Microsoft Rewards quiz answers (February 7th, 2025), numerous online tools and printable worksheets, including PDF formats, offer practice and solutions.
Online Graphing Calculators
Several online graphing calculators are invaluable tools for visualizing exponential functions, mirroring the interactive nature of Microsoft Rewards quizzes (mentioned on December 4th, 2021). Desmos and GeoGebra are excellent choices, allowing users to input equations like y = a * bx and instantly see the resulting graph. These platforms help confirm solutions found on worksheets, particularly those in PDF format, and aid in understanding transformations.
Users can experiment with different values for ‘a’ and ‘b’ to observe the impact on the graph’s shape and asymptote, similar to completing quiz questions. These calculators often provide features to plot points, find intercepts, and analyze function behavior, enhancing comprehension beyond static worksheets. They are accessible and offer immediate feedback, supporting self-paced learning and problem-solving.
Free Printable Worksheets (PDF)
Numerous websites offer free, printable worksheets in PDF format for practicing graphing exponential functions, echoing the quiz format discussed on April 5th, 2024. These resources often include a variety of problems, ranging from basic graphing to identifying key features like asymptotes and intercepts. Many worksheets also provide answer keys, allowing for self-assessment and immediate feedback, similar to the green checkmarks received on completed Microsoft Rewards quizzes.
Searching for “exponential functions worksheet with answers PDF” yields options from sites like Kuta Software and Math-Drills. These PDFs are easily downloadable and printable, making them convenient for classroom use or independent study. They complement online tools and provide a tangible way to reinforce concepts, much like the daily challenges offered through Microsoft Rewards.
Answer Keys for Worksheets
Locating answer keys is crucial for effective practice, mirroring the immediate feedback sometimes experienced with Microsoft Rewards quizzes, as noted on December 4th, 2021. Many websites offering exponential function worksheets also provide corresponding answer keys, often as a separate PDF download. These keys allow students to verify their solutions and identify areas needing improvement.
Sites like Kuta Software typically include answer keys with their worksheet offerings. When searching for “exponential functions worksheet with answers PDF,” prioritize resources that explicitly state the availability of solutions. Even if a key isn’t directly provided, online forums and educational websites may offer solutions submitted by other users, fostering a collaborative learning environment, similar to the community support found in Microsoft Rewards discussions.

Applications of Exponential Functions
Like the popular Buffalo Chicken Dip recipe from February 7th, 2025, exponential functions model real-world scenarios, including compound interest and population growth calculations.
Compound Interest Calculations
Referencing the Microsoft Rewards quizzes from December 4th, 2021, and October 12th, 2025, understanding exponential growth is crucial for financial literacy. Compound interest, a core financial concept, is perfectly modeled by exponential functions. The formula A = P(1 + r/n)^(nt) demonstrates this, where A is the future value, P the principal, r the annual interest rate, n the compounding frequency, and t the time in years.
Solving problems involving compound interest requires applying this function. For example, calculating the future value of an investment or determining the time needed to reach a specific financial goal. Like a well-executed Buffalo Chicken Dip recipe (February 4th, 2025), precise calculations yield satisfying results. Exponential functions provide the tools for these essential financial projections.
Modeling Population Growth
Drawing parallels to the engaging Microsoft Rewards quizzes mentioned on April 5th, 2024, and May 4th, 2024, exponential functions effectively model population growth. Initially, growth may seem slow, but as the population increases, the rate of growth accelerates – mirroring the popularity of a well-received Buffalo Chicken Dip (October 12th, 2025!).
The basic model is P(t) = P₀e^(kt), where P(t) is the population at time t, P₀ is the initial population, k is the growth rate, and e is Euler’s number. Analyzing this function allows predictions about future population sizes. Like troubleshooting a bugged quiz (December 4th, 2021), understanding the parameters is key to accurate modeling and forecasting population dynamics.
